고정 헤더 영역
상세 컨텐츠
본문
[알고리즘/DP/JAVA] 백준 2193 - 이친수
문제 : 백준 2193 - 이친수
문제 : https://www.acmicpc.net/problem/2193
2193번: 이친수
0과 1로만 이루어진 수를 이진수라 한다. 이러한 이진수 중 특별한 성질을 갖는 것들이 있는데, 이들을 이친수(pinary number)라 한다. 이친수는 다음의 성질을 만족한다. 이친수는 0으로 시작하지 않
www.acmicpc.net
사용언어 : JAVA
시간제한 : 2초
메모리 제한 : 128 MB
문제 설명
이진수 숫자 중 아래 성질을 만족하는 수들을 이친수라고 한다.
이친수 조건
- 이친수는 0으로 시작하지 않는다.
- 이친수에서는 1이 두 번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다.
숫자 n이 주어질 때 n자리의 이친수 갯수를 구해야하는 문제이다.
입력
첫째 줄에 N이 주어진다. (1 <= n <= 90)
예제 입력
3
출력
N 자리 이진수의 이친수 갯수를 출력한다.
예제 출력
2
사용된 알고리즘
사용된 알고리즘 : DP(동적 계획법, Dynamic Programming)
DP란 특정 문제를 풀기 위해 여러 하위 문제들로 나눈 뒤, 하위 문제들의 해결법을 저장하고 그를 사용하는 문제 해결 방식이다.
아래는 N에 따른 이친수의 수이다.
- N = 1, 1
- N = 2, 1
- N = 3, 2
- N = 4. 3
- N = 5, 5
- N = 6, 8
- N = 7, 13 ...
이 수를 들여다 볼 경우 아래와 같은 수식을 도출 할 수 있다.
$F_{n} = 1$ (n == 1 or n == 2)
$F_{n} = F_{n-1} + F_{n-2}$ (n > 2)
문제 특성상 n의 범위가 한정되어 있다. 이럴 때 크기가 90인 배열을 활용하여 문제를 풀이할 수 있다. 크기가 90인 정수 배열을 선언하고 크기가 1, 2 일 때 이친수 수가 1임을 초기화 해주기위해 0번, 1번 배열에 1을 할당한다.
그 후 반복문을 사용하여 [i]번 째 배열을 [i - 2]번 배열의 수 + [i - 1]번 배열의 수로 할당한다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
//배열 선언
int[] arr = new int[90];
//f(1) = 1, f(2) = 1
//n > 2; f(n) = f(n-2) + f(n - 1)
//크기 1, 2 일 때 초기화
arr[0] = 1;
arr[1] = 1;
//일종의 DP, 이전 크기의 이친수 수 이용하여 결과 도출
for (int i = 2; i < 90; i++) {
arr[i] = arr[i - 2] + arr[i - 1];
}
System.out.println(arr[n-1]);
}
}
이 수식은 바로 피보나치 수열과 거의 동일한 형태이다. 즉 이 문제와 유사하다.
문제의 주요 오답
위 코드를 제출하면 정답일까? 아쉽게도 아니다.

그렇다면 어디에서 오답이 발생하는 걸까?
n = 90일 경우의 결과값을 출력해보자. 아래와 같이 -1581614984라는 음수값이 출력됨을 확인할 수 있다.
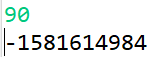
이는 n=90일 경우의 결과값이 정수형 자료형 int의 표현 가능 범위인 - 2147483648 ~ 2147483648를 벗어나 오버플로우가 발생하였기 때문에 값이 왜곡되어 출력되게 된다. 이를 해결하기 위해 int가 아닌 long 배열로 선언한다면 결과값이 long 표현 가능 범위에 들어가기 때문에 정상적으로 출력되는 것을 확인할 수 있다.
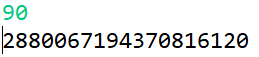
문제의 해답
해답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
// TODO Auto-generated method stub
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
//배열 선언
long[] arr = new long[90];
//f(1) = 1, f(2) = 1
//n > 2; f(n) = f(n-2) + f(n - 1)
//크기 1, 2 일 때 초기화
arr[0] = 1;
arr[1] = 1;
//일종의 DP, 이전 크기의 이친수 수 이용하여 결과 도출
for (int i = 2; i < 90; i++) {
arr[i] = arr[i - 2] + arr[i - 1];
}
System.out.println(arr[n-1]);
}
}
참고
1. 위키백과 - 동적 계획법,
https://ko.wikipedia.org/wiki/%EB%8F%99%EC%A0%81_%EA%B3%84%ED%9A%8D%EB%B2%95
동적 계획법 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
[알고리즘/재귀호출/Python] 백준 2747 - 피보나치 수
문제 : 2747번: 피보나치 수 (acmicpc.net) 2747번: 피보나치 수 피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의
potato-idiot.tistory.com
'공부 > 알고리즘' 카테고리의 다른 글
| [BFS / 알고리즘] BFS에서 방문처리가 의미하는 것 (0) | 2023.03.09 |
|---|---|
| [알고리즘/브루트포스/JAVA] 백준 1107 - 리모컨 (1) | 2023.03.06 |
| [알고리즘/재귀호출/Python] 백준 2747 - 피보나치 수 (0) | 2022.03.16 |
| [알고리즘/계수정렬/Python] 백준 10989 - 수 정렬하기 3 (0) | 2022.03.16 |
| [알고리즘/Union-Find/Python] 백준 4195 - 친구 네트워크 (0) | 2022.03.12 |





